Un modelage ou une sculpture c'est avant tout une forme dans l'espace, et comme laplupart d'entre elles une forme qui présente une courbure.,lorsqu'on travaille avec des colombins , tout est assez intuitif, avec des plaques on est obligé de se poser quelques questions à propos de la géométrie des pièces qu'on va être amené à préparer .

La terre est souple bien sur , et elle permet des "déformations que la forme plane de départ n'aurait pas permis sans cela, mais cependantr si on sait quelle forme doivent avoir les plaques de départ c'est plus facile.

Pour moi , la révélation de la courbure c'est un certain Jean pierre Petit qui me l'a donnée .(il est vrai que je l'avais entrevu avantpar des moyens moins "didactiques").Jean pierre Petit est l'auteur d'aventures en BD bien interessantes :"le Géométricon de Lanselme Lanturlu "mais c'est là une autre histoire.e

Pour simplifier il y a des formes dans l'espace qi n'ont pas de courbure comme un cylindre ,et d'autres qui ont une courbure comme un cône . C'est d'ailleurs par là que je commence.

(la courbure d'une surface autour d'un point se mesure en angle .Quel est cet angle?

Imaginons une feuille de papier sur laquelle on a ôté un secteur d'angle , on relie les bords et on obtient

un cône.

la courbure autour du sommet du cône est d'angle  signifie qu'on a enlevé un angle  à la surface plane qui a servi à constituer ce cône.

exemples

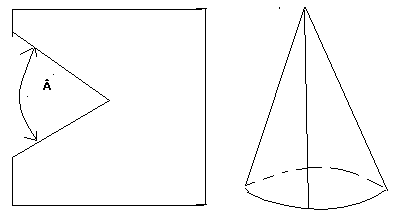Comment calculer la forme exacte d'un gabarit qui doit reproduire un cône d'angle au sommet teta et de rayon a la base r :ce cône aura une arête R et cette forme sera du genre de celle ci :

 
 

Le cas réel de la tasse ou du saladier qui a en gros la forme d'un tronc de cône est un peu plus difficile mais guère:

En cliquant ici vous lancez un petit programme qui vous donnera toutes les dimentions du gabarit à dessiner pour ce tronc de cône

 

considérons maintenant la partie inférieure d'une boite à chaussures :développée à plat elle a cette forme:

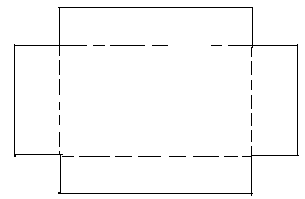les 4 coins à angle droits qui ont été retirés confèrent à la boite reconstruite

une courbure totale de 360°. Si nous avions continué à dessiner la forme développée d'une boite complètement fermée nous aurions eu 720° de courbure.

Donc ,si le fond d'un plat (on fait de la poterie non?) ou d'une boite est plat et que nous voulons avoir des bords qui soient

verticaux il faut prévoir une courbure de 360° .

Voyons sur 2 exemples ce que ça donne.

Une boite de fond triangle équilatéral à bords vericaux.

Si nous avions choisi une boite à fond exagonal ,à chaque coin il aurait fallu couper un secteur d'angle de 360/6=60°

 

 

Maintenant si nous désirons seulement avoir les bord de la boite à 45° :la courbure totale étant de 180° il aurait fallu dans le cas de la boite à chaussure n'enlever à chaque coin qu'un secteur de 45°

Dans le cas du fond triangulaire 60°

Dans le cas de l'hexagone 30°

 

  

 

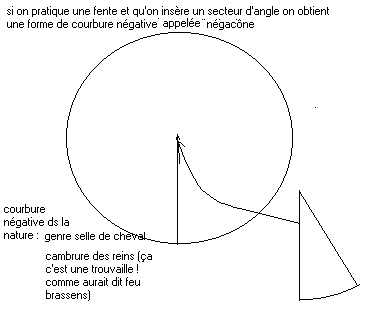
Bon mais la courbure n'est pas toujours "positive":comme un ballon, une fesse,une goutte d'eau (qui en passant n'a pas 720° de courbure, elle).

Il y a aussi des courbures "négatives" (enfin pas à tous points de vue) comme la selle d'un cheval , la cambrure des reins etc..

Alors celles là ? he bien sur la surface plane, si au lieu "d'enlever un secteur d'angle" comme pour le cône ci dessus on rajoute un secteur d'angle, on obtient des formes bizzaroides qu'on nomme "négacônes"